黄金比という言葉を、
みなさんもどこかで聞いたことがあるかと思います。

この黄金比は、およそ

なのですが、

もっとも美しい長方形の比率として、
企業のブランドロゴや、
名刺、ウェブサイトのデザインなどに使われています。

でもなぜ、1：1.618..？
誰が決めたの？
どうやって計算すればいいの？

。。。ですよね。

今回は、
そんな沸き起こる皆様の疑問に、
わかりやすくお答えしたいと思います。

どうぞごゆっくりお楽しみください。

スポンサードリンク
[ad#recl]

黄金比の発見者　レオナルド・フィボナッチ

今でも日常的に使用されているこの黄金比、
実はその歴史はとても古いのです。

発見者は、イタリアの天才数学者、
レオナルド・フィボナッチ。

彼は、1202年に次のような数列を発見しました。

フィボナッチは、
うさぎのつがいの生まれ方から、
この数列を発見しました。

不思議なことに、この数列の
隣り合う2数の和は、その次の数と等しくなります。

０＋１　　　　１
１＋１　　　　２
１＋２　　　　３
２＋３　　　　５
３＋５　　　　８
５＋８　　　１３
８＋１３　　２１
１３＋２１　３４
２１＋３４　５５
。
。
。

フィボナッチ数列から黄金比を導く

そして、隣あう2数の比率は、
だんだん黄金比、1.618…に近づいていきます。

2÷1=2.0
3÷2=1.5
5÷3=1.66666
8÷5=1.6
13÷8=1.625
21÷13=1.6153
34÷21=1.6190
55÷34=1.6176
89÷55=1.6181
144÷89=1.6179
233÷144=1.6180

おもしろいですね！

また、
X2-X-1=0
という２次方程式の解からも、
黄金比を求めることができますよ。

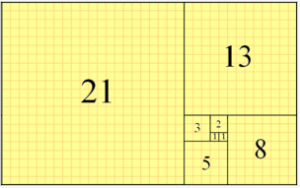
黄金比をもつ長方形の簡単な描き方

それでは、実際に黄金比の長方形を描いてみましょう！

１．１辺を１とする正方形を二つ並べる。
２．２つ並んだ正方形の長いほうの辺を一辺として、一辺２の正方形を描く。
３．一辺が１と２の正方形、つまり一辺３の正方形を描く。
４．一辺３と一辺２の正方形、つまり一辺５の正方形を描く。

このように続けていくと、
上のような長方形がいくつも描けます。
どの長方形も、全て黄金比の長方形です。

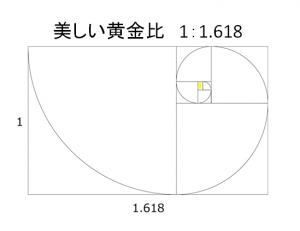
そして正方形の一辺を半径とした弧を描いていくと、
美しいらせん模様が描けます。

自然界のフィボナッチ数列

黄金比を持つフィボナッチ数列や、
そのらせん模様は、
実は自然界にたくさん現れているのです。

例えば、
松ぼっくりやヒマワリの種、
オウムガイの巻いた部分。
樹木の葉の付き方。

フィボナッチさんも、
ウサギのつがいの生まれ方から
この数列を導いたそうです。

自然界で最も適応力を発揮するような
「数のパターン」なのかもしれませんね。

次の動画は、フィボナッチ数列についての動画です。

興味を持たれた方は、
是非ご覧ください。

こちらは、日本の文部科学省作成の動画です。
とても分かりやすいですよ。

お付き合いいただきありがとうございました。
自然って本当に不思議ですね！